Imagine a world where numbers dance and calculations transform into captivating journeys. Our journey today takes us to the intriguing realm of exponents, where we explore the power of 6 to the fourth. It might sound like a simple mathematical expression, but the story behind it is far more captivating than you might suspect.

Image: www.quia.com
This exploration delves into the world of exponentiation, a fundamental concept in mathematics. It involves multiplying a number, known as the base, by itself a certain number of times, called the exponent. In our case, we’re diving into the world of 6 to the power of 4, which signifies 6 multiplied by itself four times. But why is this concept so fascinating? What secrets lie within this seemingly simple equation?
Unveiling the Power of Exponents
At its core, exponents offer a shortcut for expressing repeated multiplication. Instead of writing 6 x 6 x 6 x 6, we can simply write 64. This elegant notation streamlines complex calculations and makes them easier to understand. Picture a scenario where you need to calculate the volume of a cube with each side measuring 6 units. Using exponents, we can quickly determine the volume as 63 or 216 cubic units.
Diving into the History of Exponents
The concept of exponents has a rich history, stretching back centuries. Early civilizations, including the Babylonians and Egyptians, used their own notations to represent repeated multiplications. However, the modern notation we use today, with the base and exponent, can be traced back to the 17th century, with the works of French mathematician René Descartes.
Descartes’ work revolutionized the way exponents were written and understood, leading to their widespread adoption in scientific and mathematical fields. This standardized notation helped simplify calculations and laid the foundation for further mathematical advancements.
Unraveling the Mysteries of 6 to the Power of 4
Let’s focus specifically on 64. Calculating this expression, we find that it equals 1296. This number, on the surface, might not seem particularly remarkable. Yet, it holds intriguing connections to various mathematical concepts and real-world applications.
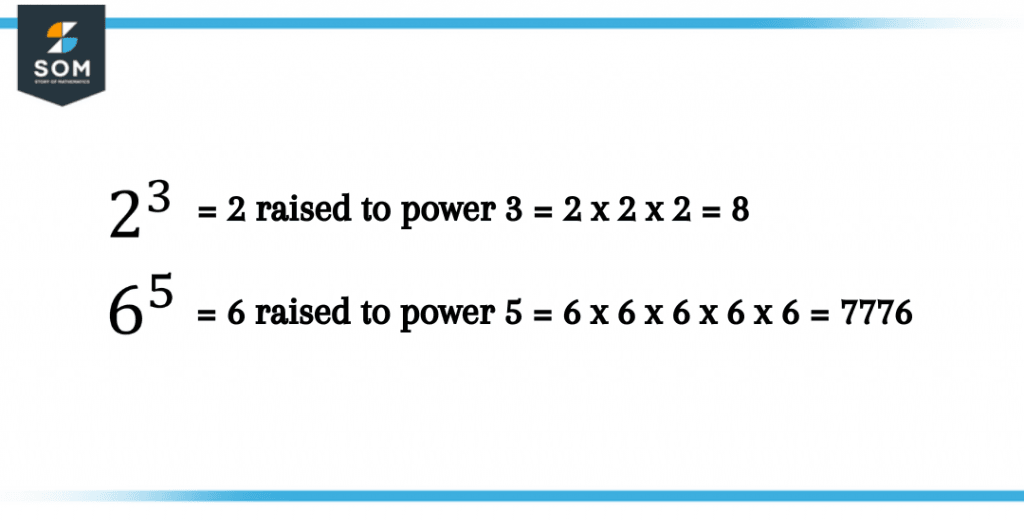
Image: www.storyofmathematics.com
Exploring the World of Prime Factorization
When we break down 1296 into its prime factors, we find that it is composed of 24 x 34. This prime factorization reveals a unique pattern in the number’s structure. The factors 2 and 3, each raised to the power of 4, highlight the underlying relationship between prime numbers and the concept of exponents.
Exploring the Math Behind Combinations
The concept of combinations, which involves counting the number of ways to choose items from a set, is deeply connected to exponents. Imagine a situation where you have 6 different colors of paint, and you need to choose 4 colors to paint a room. The number of possible combinations in this case is dictated by the formula 64.
The exponential nature of combinations underlines how quickly the number of possibilities can grow when you have a large set of choices. This concept finds numerous applications in fields like statistics, probability, and computer science.
The Real-World Significance of 6 to the Power of 4
While 64 might seem like an abstract mathematical concept, its applications extend far beyond the confines of textbooks. Let’s explore some real-world examples where this seemingly simple calculation holds significant relevance:
The World of Computer Science
In computer science, where data is often represented in binary form (0s and 1s), exponents play a crucial role in understanding memory capacity and processing power. A common unit of data storage is the byte, which consists of 8 bits. Therefore, a kilobyte (KB) is equal to 210 bytes, which translates to 1024 bytes.
The use of exponents in computer science makes it easier to express and manipulate large quantities of data, simplifying a complex field. This is why we often see numbers like 210, 220, or 230 used to represent various units of data storage and processing power.
Expanding Horizons in Biology
Interestingly, exponents also emerge in the realm of biology. Imagine a single bacterium that replicates every hour. This single cell, after 4 hours, would have multiplied to 24 or 16 bacteria. Exponents become crucial tools for understanding exponential growth and its impact on population dynamics.
The rapid growth of bacterial populations, often fueled by the availability of nutrients and resources, demonstrates the power of exponents to describe and predict real-world phenomena. Similar concepts apply to the growth and spread of other organisms, highlighting the relevance of mathematical principles in diverse fields.
6 To The Power Of 4
The Power of 6 to the Power of 4: A Lasting Impact
From its historical roots in ancient civilizations to its modern applications in computer science and biology, 64, or 1296, embodies a profound concept that continues to shape various fields. It represents a journey of mathematical discovery, showcasing the beauty and power of exponents in unraveling the mysteries of the world around us.
As you delve deeper into the world of mathematics, remember the fascinating power of exponents. They are more than just simple numerical operations; they are keys to understanding intricate patterns and solving complex problems across diverse disciplines.





