Have you ever looked at a graph and wondered about the steepness of a line? The incline or decline of that line is what we call “slope,” and it plays a crucial role in various fields, including mathematics, physics, and even economics. But what exactly does “slope 4” mean, and how does it relate to other slopes? This article dives deep into the world of slope 4, exploring its definition, implications, and practical applications.
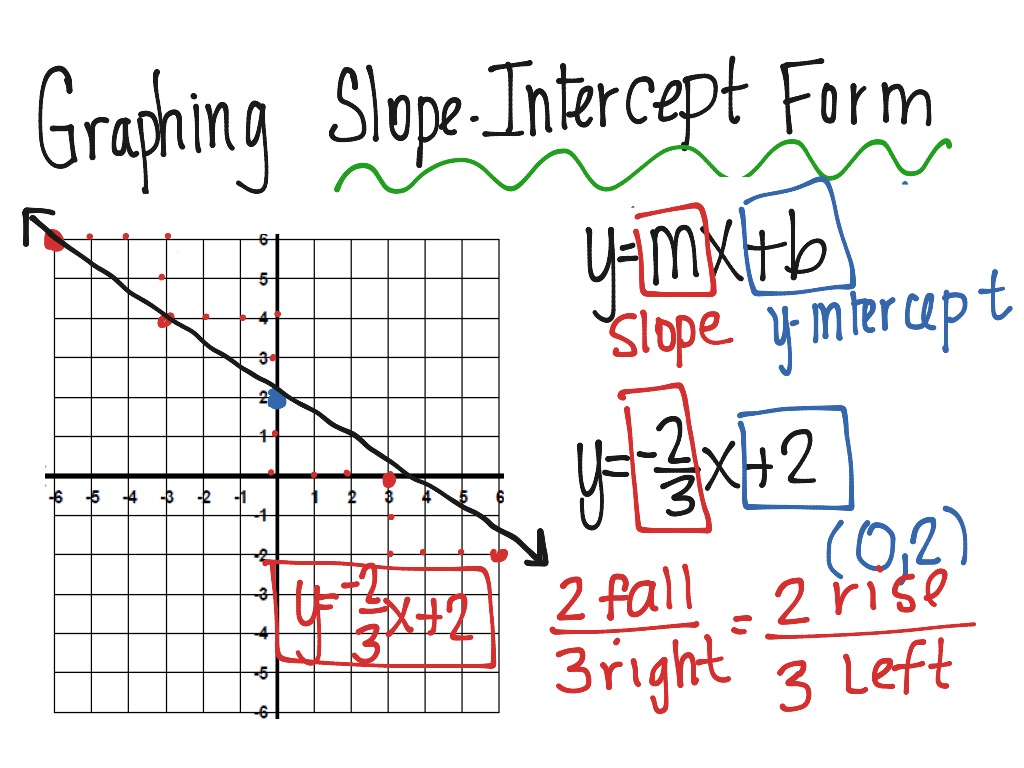
Image: www.showme.com
Imagine you’re hiking up a mountain. The trail might have some gradual sections, some steeper inclines, and possibly even some flat stretches. Each of these sections represents a different slope, and the “slope 4” is like the steepest incline you could encounter, making your hike quite challenging!
Understanding Slope 4: A Foundation in Mathematics
Defining Slope
Before we delve into slope 4, let’s first understand the concept of slope itself. In mathematics, slope refers to the measure of the steepness or incline of a line. It represents the ratio of the vertical change (rise) to the horizontal change (run) between any two distinct points on that line. The slope is often expressed as a fraction, where the numerator represents the rise, and the denominator represents the run.
Slope 4 Explained
Now, let’s get to the heart of the matter: Slope 4. This simply means that for every 1 unit you move horizontally (run), you move 4 units vertically (rise). So, if you start at a point on a line with a slope of 4, and move right by 1 unit, you would have to move up by 4 units to stay on the line. The larger the value of the slope, the steeper the incline.
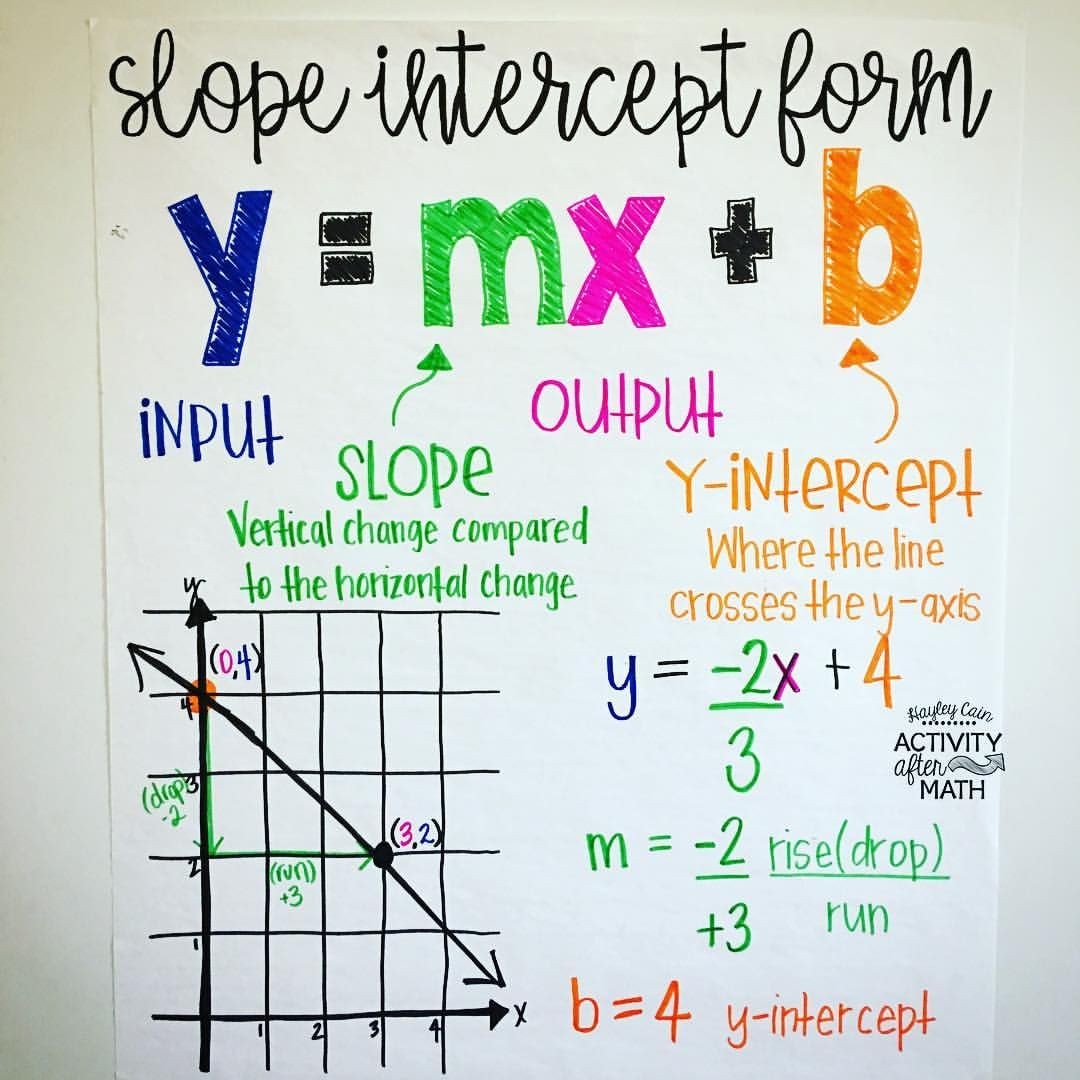
Image:
Slope 4 in the Real World
You might be surprised to learn that slope 4 isn’t just an abstract mathematical concept. It has real-world applications in various fields:
- Construction: When building roads, bridges, and ramps, engineers must consider the slope to ensure safety and stability. A slope of 4 would indicate a very steep incline or decline, requiring specific design considerations.
- Geography: The terrain of mountains and hills can be represented using slope values. A slope of 4 would indicate a challenging, steep terrain that would require considerable effort to traverse.
- Finance: In financial markets, the concept of slope helps to measure the rate of change in prices over time. A steep slope (like slope 4) would indicate a rapid increase or decrease in value.
- Art: Artists use perspective and slope to create depth and realism in their works. A slope of 4 could be used to represent a strong sense of perspective in a drawing.
Slope 4: Implications and Applications
The concept of slope 4 goes beyond just defining the steepness of a line. It also has several implications and applications in various fields, some of which we’ve already mentioned. For instance, when applied to the graph of a function, the slope represents the rate of change of that function. Higher slopes indicate faster rates of change. This concept is crucial in fields like physics, where it is used to describe the velocity and acceleration of objects.
In economics, the slope of the demand curve can be used to understand the relationship between the price of a good and the quantity demanded. A slope of 4 would suggest a highly elastic demand, meaning that a small change in price would lead to a large change in the quantity demanded.
Keeping Up with Trends in Slope 4
Evolving Applications of Slope
The applications of slope concepts are constantly evolving. With the advent of new technologies, we are seeing slope being used in even more innovative ways. In computer graphics, for instance, slope is employed to create realistic lighting effects and shadows. This means understanding slope isn’t just important for mathematicians and engineers, but also for graphic designers and game developers.
Emerging Technologies and Slope
One exciting development is the application of slope in artificial intelligence (AI). Machine learning algorithms often rely on the concept of slope to optimize their performance. By understanding the “slope” of the learning process, AI systems can adjust their parameters to find the optimal solution. This has resulted in significant advancements in fields like image recognition, natural language processing, and robotics.
Expert Tips for Grasping Slope 4
Visualize the Concept
One of the most effective ways to understand slope 4 is to visualize it. Draw a graph, and use a ruler to draw a line. Then, use the concept of rise over run (4/1) to mark points on the line. This will help you see the steepness of the slope in action.
Use Real-World Examples
Connecting mathematical concepts to real-world scenarios can make them more engaging and easier to grasp. When learning about slope 4, think about hills, mountains, or even ramps in your daily life. Observe their slopes, and try to estimate their values to improve your understanding.
Practice, Practice, Practice!
The key to mastering any mathematical concept, including slope, is practice. Solve problems, work through examples, and apply your knowledge to real-world scenarios. You can even use online resources like Khan Academy or Youtube videos to enhance your learning through practice and tutorials.
FAQ: Slope 4 and Beyond
Q: What is the difference between a positive and a negative slope?
A: A positive slope indicates an upward incline, while a negative slope indicates a downward decline. The value of the slope (i.e., 4) simply refers to the steepness of that incline or decline.
Q: Are all slopes linear?
A: No, slopes can be linear (a straight line) or nonlinear (curved). A slope of 4, however, refers to a linear slope.
Q: What are some other important slope values to know?
A: Besides slope 4, there are other crucial slope values you might encounter. Slope 0 represents a horizontal line, while an undefined slope represents a vertical line.
Q: How can I calculate the slope of a line if I know its equation?
A: The slope of a line can be determined from its equation. For example, if the equation is y = 4x + 2, then the slope is 4. The coefficient of the x term represents the slope.
Q: What are some resources for learning more about slope?
A: Many resources can deepen your understanding of slope, including textbooks, online courses, and educational websites like Khan Academy. You can also explore instructional videos on platforms like YouTube.
Slope 4
Conclusion: Slope 4 and the Power of Geometry
Understanding slope 4 is not just a matter of knowing a mathematical concept; it’s about appreciating its relevance and applications in our world. From engineering to finance, art to AI, slope plays a critical role in shaping our understanding of various disciplines. By grasping this fundamental concept, we can better analyze and interpret the world around us.
Are you intrigued by the power of slope 4 and its vast applications? Let us know in the comments below. We’d love to hear your thoughts and any questions you may have about this fascinating mathematical topic!





