The square root of 240 might seem like a simple concept, a mere mathematical operation. But delve deeper, and you’ll discover a world of fascinating properties and historical significance. I remember the first time I encountered this number during my algebra class. My teacher challenged us to find its value, and I was stumped. It wasn’t a perfect square like 4 or 9. The quest to unravel the mystery of the square root of 240 ignited a curiosity in me that I haven’t forgotten.

Image: prezi.com
Today, I want to share this journey of discovery with you. We’ll explore the ins and outs of calculating the square root of 240, understand its mathematical significance, and even touch upon its relevance in the real world. Let’s embark on this journey together and unravel the intriguing nature of this seemingly simple number.
Understanding Square Roots: A Foundation for Exploration
Before diving into the nitty-gritty of the square root of 240, let’s revisit the basics of square roots. In essence, the square root of a number is the value that, when multiplied by itself, equals the original number. For example, the square root of 9 is 3 because 3 multiplied by 3 equals 9. However, not all numbers have perfect squares, like the square root of 240.
Numbers like 240, whose square roots cannot be expressed as whole numbers, are called irrational numbers. They have an infinite decimal representation that doesn’t repeat. This means the square root of 240 can only be approximated to a certain degree of accuracy. Thankfully, we have several methods to calculate such numbers effectively.
Calculating the Square Root of 240: Unveiling the Mystery
One common way to find the square root of 240 is through factorization, simplifying the problem into smaller parts. Let’s break down the process:
- Prime factorization: We start by factoring 240 into its prime factors: 240 = 2 x 2 x 2 x 2 x 3 x 5.
- Grouping factors: We pair up the prime factors as much as possible: 240 = (2 x 2) x (2 x 2) x 3 x 5.
- Extracting square roots: We extract the square root of each paired factor. The square root of (2 x 2) is 2, so we get: 2 x 2 x √(3 x 5).
- Simplifying the result: Multiplying the numbers outside the square root, we obtain the simplified form: 4√15.
Therefore, the square root of 240 can be written in simplified form as 4√15. While not a whole number, this representation provides a more concise and accurate understanding of the number.
Another method involves using a calculator. Most calculators have a square root function that allows you to readily calculate the square root of 240. The result will be a decimal number, often rounded to a few decimal places, giving you an approximation of the square root. While this method is simpler, it doesn’t offer the insight into the number’s composition that factorization provides.
Understanding the square root of 240 goes beyond simply finding its numerical value. The concept of square roots has far-reaching implications in various fields, from basic geometry to advanced mathematics.
Beyond the Basics: The Square Root of 240 in Real-World Applications
While the square root of 240 might not seem immediately relevant to our daily lives, it finds its applications in various fields. Consider geometry, where calculating the diagonal of a rectangle or the hypotenuse of a right triangle often requires finding the square root of a number, potentially including the square root of 240. This demonstrates that understanding square roots is essential for tackling real-world problems.
Furthermore, the square root of 240 plays a role in various engineering and physics applications. For example, in calculating the velocity of an object influenced by gravity, square roots are employed. This emphasizes the importance of understanding square roots in various scientific disciplines.
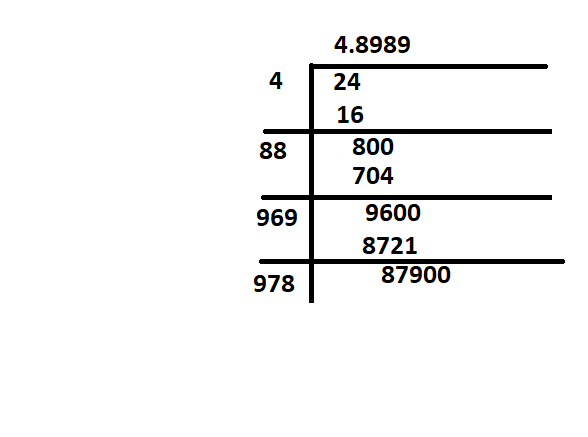
Image: stacklima.com
Current Trends and Developments: Expanding Our Understanding
The concept of square roots and irrational numbers continues to be explored by mathematicians and scientists. Current research delves into the complexities of irrational numbers, investigating their properties, and exploring their applications in various fields.
One exciting development is the utilization of computational tools to approximate irrational numbers like the square root of 240 with increasing precision. These advancements allow us to gain deeper insights into the nature of these numbers and their applications. This is particularly important in fields like physics and engineering, where accurate calculations are essential.
Tips and Expert Advice: Mastering the Square Root of 240
Here are some expert tips to enhance your understanding of the square root of 240:
- Practice factorization: Consistently practicing prime factorization will make you more comfortable with breaking down numbers and simplifying expressions involving square roots.
- Explore different methods: Don’t limit yourself to one method of calculating square roots. Experiment with using a calculator and exploring online tools to find different approaches.
- Visualize the concepts: Engaging your visual senses can be helpful. Try drawing diagrams or using online tools to visualize the process of finding square roots, which can improve your understanding.
- Embrace the challenge: Square roots can be challenging, but don’t be discouraged. The more you practice and explore, the more comfortable you’ll become with these concepts.
By following these tips, you can deepen your understanding of the square root of 240 and explore the realm of square roots with confidence.
Frequently Asked Questions (FAQs)
Q: Is the square root of 240 a rational or irrational number?
A: The square root of 240 is an irrational number because it cannot be expressed as a fraction of two integers. It has an infinite decimal representation that doesn’t repeat.
Q: What are some applications of square roots in real-world problems?
A: Square roots are used in geometry to calculate the diagonal of a rectangle or the hypotenuse of a right triangle, in physics to calculate velocity and acceleration, and in engineering for various calculations involving forces and distances.
Q: Can the square root of 240 be simplified further than 4√15?
A: No, 4√15 is the most simplified form of the square root of 240. The numbers outside the square root (4) and inside the square root (15) have no common factors that can be further simplified.
Square Root Of 240
Conclusion
The square root of 240, while seemingly simple, is a fascinating and multifaceted number. Understanding its calculation, its significance in various fields, and the ongoing research into irrational numbers helps us appreciate the beauty and complexity of mathematics. Remember, the key to mastering this topic lies in practice, exploration, and embracing the challenge. Are you interested in learning more about the square root of 240 and exploring its intricacies further?





