Have you ever found yourself in a situation where you needed to figure out what percentage one number represents of another? This is a common task in many aspects of life, from figuring out your score on a test to calculating sales discounts. One such question that often arises is: “What percent of 5 is 3?” This seemingly simple question can reveal a lot about our understanding of percentages and how to perform basic calculations. In this article, we’ll dive deep into the world of percentages, explore the methods to solve this problem, and understand its implications in various real-world scenarios.
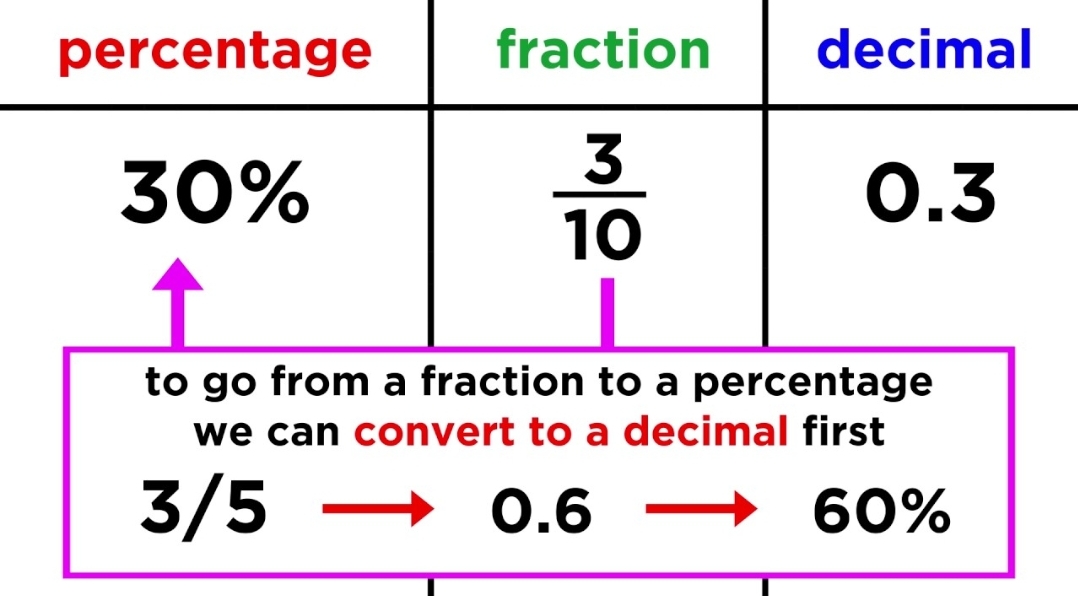
Image: www.kidibot.com
Imagine you’re at a bakery, eyeing a delicious chocolate cake. The baker tells you that it’s 5 pounds and you want to buy only 3 pounds. How do you explain to the baker how much of the whole cake you want to purchase? This is where percentages come in handy. By figuring out what percentage 3 pounds represents of the whole 5 pounds, you can clearly express your desire to buy 60% of the cake. This scenario highlights the importance of percentages in everyday life, especially when dealing with quantities and proportions.
Understanding Percentages as a Representation of the Whole
Percentages are a powerful tool for representing parts of a whole. Essentially, they express a fraction out of 100. The word “percent” means “out of one hundred,” represented by the symbol %. Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. This understanding is crucial when calculating what percentage one number represents of another.
To find the percentage, we need to determine the proportion of the smaller number (in this case, 3) relative to the larger number (5). In other words, we need to find the fraction that 3 represents of 5, then express that fraction as a percentage.
Methods to Calculate What Percent of 5 is 3
Method 1: Using the Fraction and Multiplication
1. Set up the fraction: Divide the smaller number (3) by the larger number (5), which gives you 3/5.
2. Convert to a decimal: Divide the numerator (3) by the denominator (5), resulting in 0.6.
3. Multiply by 100: To express the decimal as a percentage, multiply it by 100. Therefore, 0.6 x 100 = 60%.

Image: www.teachoo.com
Method 2: Using the Proportion Formula
1. Set up the proportion: We can represent the problem as a proportion: 3/5 = x/100 where x is the unknown percentage.
2. Solve for x: To solve for x, we can cross-multiply. This gives us: 3 * 100 = 5 * x, which simplifies to 300 = 5x.
3. Isolate x: Divide both sides by 5 to get x = 60.
4. Express as a percentage: x = 60 represents 60%.
Applications of Percent Calculations
The ability to calculate percentages extends far beyond simple cake purchases. It finds application in various fields, including:
- Finance: Calculating interest rates, loan repayments, and investment returns.
- Retail: Determining discounts, sales tax, and markups on products.
- Statistics: Analyzing data, calculating probabilities, and representing trends.
- Health and Nutrition: Calculating body mass index (BMI), calorie intake, and nutritional information.
- Education: Grading assignments, evaluating test scores, and understanding student performance.
Tips and Expert Advice on Using Percentages
Here are some tips for mastering percentages and applying them effectively:
- Practice regularly: The more you practice percentage calculations, the more comfortable you’ll become with the concepts.
- Utilize online resources: Many websites offer free calculators and tutorials to help you with percentage calculations.
- Visualize percentages: Creating mental images can help you understand the relationship between percentages and whole numbers.
- Break down complex problems into simpler steps: If you’re faced with a complicated problem, break it down into smaller, easier-to-manage steps.
- Always check your answers: Be sure to double-check your calculations to avoid errors.
When applying percentages in real-world situations, remember that the context is crucial. For instance, calculating a discount on a product requires careful attention to the base amount and the percentage discount, while calculating interest rates involves taking into account the principal amount, the interest rate, and the time period.
FAQ
Q: What is the meaning of “percent”?
A: “Percent” means “out of one hundred.” So, 50% represents 50 out of 100.
Q: Why is it important to understand percentages?
A: Percentages are widely used in various fields, from finance and retail to health and education. They provide a standardized way to represent parts of a whole, making it easier to compare different quantities and proportions.
Q: Can I use a calculator to calculate percentages?
A: Yes, calculators can efficiently handle percentage calculations, especially for complex problems. However, it’s still essential to understand the underlying concepts to interpret the results correctly.
Q: How can I improve my understanding of percentages further?
A: You can explore online tutorials, watch educational videos, or consult textbooks on mathematics and statistics. There are countless resources available for enhancing your knowledge of percentages.
What Percent Of 5 Is 3
Conclusion
In this article, we explored the topic of “What percent of 5 is 3?”. We discovered that the answer is 60%, meaning that 3 represents 60% of 5. Understanding percentages is essential for various aspects of life, from everyday shopping to complex financial calculations. By mastering the methods of percentage calculation and practicing regularly, you can confidently apply this valuable concept in diverse situations.
Are you interested in learning more about percentages, or do you have any other percentage-related questions you’d like to explore? Share your thoughts and inquiries in the comments below!





