Have you ever found yourself in a situation where you needed to find the lowest common multiple (LCM) for two numbers, like 9 and 15? Maybe you’re trying to plan a party where you need enough food and drinks for both 9 people and 15 people, and you want to ensure you have enough without having any leftovers. Or perhaps you’re working on a project that involves coordinating tasks that take 9 minutes and 15 minutes to complete, and you want to figure out the shortest amount of time it takes to complete both tasks simultaneously. This is where understanding the concept of LCM comes in handy.
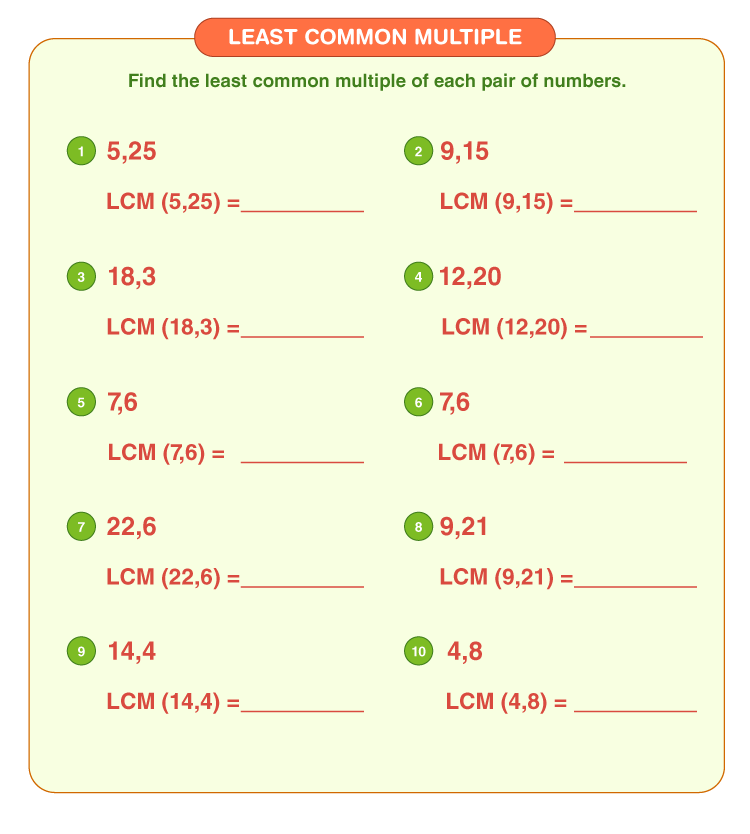
Image: millerkathleen.blogspot.com
In this article, we’ll explore the concept of LCM, specifically focusing on how to calculate the LCM for 9 and 15. We’ll delve into the methods for finding the LCM, discuss its applications, and examine related concepts to provide a comprehensive understanding of this important mathematical concept.
Understanding the Concept of LCM
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in areas like number theory and arithmetic. The LCM of two or more integers is the smallest positive integer that is a multiple of all of those integers. In simpler terms, it is the smallest number that can be divided by all the given integers without leaving any remainder.
Understanding the LCM is crucial in various applications, including:
- Fractions: When adding or subtracting fractions with different denominators, we need to find the LCM of the denominators to achieve a common denominator.
- Time and Motion: The LCM is useful in situations where we need to synchronize events with different time periods, such as scheduling meetings or coordinating tasks.
- Music: In music theory, the LCM helps determine the least common period of repeating musical patterns.
Methods for Finding the LCM
There are several methods for finding the LCM of two or more numbers, each with its own advantages and disadvantages. Here, we’ll discuss two common methods: the prime factorization method and the listing multiples method.
Prime Factorization Method
The prime factorization method involves breaking down the given numbers into their prime factors. Here’s how it works:
- Find the prime factors of each number:
- 9 = 3 x 3
- 15 = 3 x 5
- Identify common and unique prime factors:
- Both numbers share the prime factor 3.
- The unique prime factors are 3 (for 9) and 5 (for 15).
- Multiply the highest powers of all prime factors:
- The highest power of 3 is 3² (from the prime factorization of 9).
- The highest power of 5 is 5¹ (from the prime factorization of 15).
- Calculate the product:
- LCM (9, 15) = 3² x 5¹ = 9 x 5 = 45
Therefore, the LCM of 9 and 15 is 45.
Image: www.cuemath.com
Listing Multiples Method
The listing multiples method involves listing out the multiples of each number until a common multiple is found. This method is simpler for smaller numbers but becomes less efficient as the numbers get larger.
- List the multiples of the larger number:
- Multiples of 15: 15, 30, 45, 60…
- Check if the multiples of the smaller number are included:
- Multiples of 9: 9, 18, 27, 36, 45…
- 45 is a multiple of both 9 and 15.
Therefore, the LCM of 9 and 15 is 45.
Applications of LCM in Real-Life Scenarios
The LCM has various applications in everyday life, ranging from simple tasks to complex calculations. Here are some real-life examples:
Scheduling Tasks
Imagine you have two tasks to complete: one takes 9 minutes and the other takes 15 minutes. To determine when you can finish both tasks simultaneously, you need to find the LCM of 9 and 15, which is 45. This means that after 45 minutes, you will have completed both tasks, and you can start on other tasks that require the completion of both initial tasks.
Cooking Recipes
If a recipe calls for 9 eggs and another recipe calls for 15 eggs, you can find the LCM (45) to determine the minimum number of eggs needed to make both recipes without any leftovers. You’ll need to buy or use 45 eggs.
Music Theory
In music, notes are often grouped into bars or measures. To determine the shortest time interval where two musical patterns repeat simultaneously, you need to find the LCM of the number of notes in each pattern. This helps musicians coordinate their rhythms effectively.
Tips for Finding the LCM
Finding the LCM can be made easier with a few simple tips:
- Start with the larger number: When listing multiples, begin with the multiples of the larger number as it will likely have fewer multiples to check.
- Use prime factorization: For larger numbers, the prime factorization method is more efficient and less prone to errors.
- Look for common factors: If the numbers have common factors, you can use them to simplify the calculations.
By following these tips, you can find the LCM more quickly and accurately.
FAQ about LCM
Here are some frequently asked questions about LCM:
Q: What is the difference between LCM and GCD?
A: LCM (Least Common Multiple) is the smallest number that is a multiple of all the given numbers. GCD (Greatest Common Divisor) is the largest number that divides all the given numbers evenly.
Q: Can the LCM be the same as one of the original numbers?
A: Yes, if one of the original numbers is a multiple of the other. For example, the LCM of 4 and 8 is 8.
Q: Is there any shortcut for finding the LCM of two numbers?
A: For two numbers, the LCM can be calculated using the formula: LCM (a, b) = (a x b) / GCD (a, b). This formula is helpful when you already know the GCD (Greatest Common Divisor) of the two numbers.
Lcm For 9 And 15
Conclusion
In this article, we explored the concept of LCM, specifically focusing on how to calculate the LCM for 9 and 15. We learned that the LCM is the smallest positive integer divisible by all the given integers, finding its significance in various real-life applications. We also discussed two common methods for finding the LCM, the prime factorization method and the listing multiples method.
Understanding the LCM is essential in numerous mathematical concepts and practical situations. By applying the methods and tips discussed in this article, you can confidently find the LCM of any set of numbers and unlock its applications in different fields. Understanding the LCM can help simplify calculations, find solutions to various problems, and even improve your understanding of music theory.
Are you interested in learning more about LCM or exploring its various applications? Please share your thoughts and questions in the comments section below. Let’s dive deeper into this fascinating mathematical concept together!





