Have you ever wondered about the invisible thread that connects seemingly unrelated numbers? In the realm of mathematics, this invisible thread is the greatest common factor, also known as the greatest common divisor (GCD). It’s a fundamental concept that plays a crucial role in various mathematical operations and applications. Today, we embark on a journey to unravel the greatest common factor of 24 and 40, delving into its calculation, significance, and practical implications.
Image: www.cuemath.com
The greatest common factor (GCF) of two or more numbers is the largest number that divides evenly into all of them. Understanding the GCF is essential for simplifying fractions, solving problems involving ratios, and even understanding the rhythmic patterns in music. Our exploration will shed light on the techniques used to find the GCF, its practical uses, and its intriguing connections to other mathematical concepts.
Methods to Find the Greatest Common Factor
Finding the GCF of 24 and 40 involves techniques that can be adapted to any pair of numbers. Two popular approaches are:
1. Prime Factorization Method
This method relies on breaking down numbers into their prime factors. Prime factors are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11). Let’s break down 24 and 40 into their prime factors:
- 24 = 2 x 2 x 2 x 3
- 40 = 2 x 2 x 2 x 5
Now, identify the common prime factors and their lowest powers that appear in both factorizations: 2 x 2 x 2 = 8. Therefore, the GCF of 24 and 40 is 8.
2. Euclidean Algorithm
The Euclidean algorithm offers an efficient way to find the GCF using repeated division. It’s based on the idea that the GCF of two numbers is the same as the GCF of the smaller number and the difference between the two numbers. Let’s illustrate this with 24 and 40:
- 40 – 24 = 16
- 24 – 16 = 8
- 16 – 8 = 8
Since the difference is now 8, and 8 divides evenly into both 16 and 8, the GCF of 24 and 40 is 8. This algorithm is especially useful for large numbers.
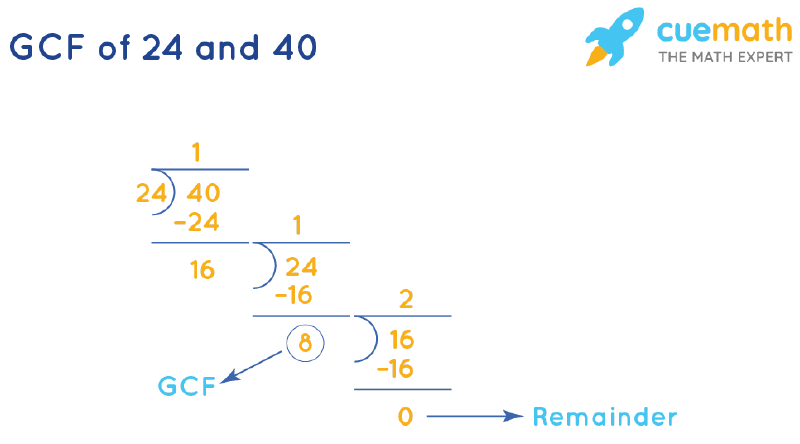
Image: www.cuemath.com
Real-World Applications of the GCF
The GCF isn’t just a theoretical concept; it finds practical application in various aspects of life:
1. Simplifying Fractions
When simplifying fractions, we divide both the numerator and denominator by their GCF. If we have the fraction 24/40, the GCF of 24 and 40 is 8. Dividing both numerator and denominator by 8 results in the simplified fraction 3/5.
2. Dividing Objects into Equal Groups
Imagine you have 24 candies and 40 cookies. You want to divide them into equal groups. The GCF of 24 and 40, which is 8, tells you the largest number of equal groups you can create. You can have 8 groups, each containing 3 candies and 5 cookies.
3. Understanding Rhythmic Patterns in Music
In music, the GCF helps understand the relationship between different time signatures. For example, a 4/4 time signature (four beats per bar) and a 3/4 time signature (three beats per bar) have a GCF of 1, indicating they are independent rhythms. On the other hand, a 6/8 time signature (six eighth notes per bar) and a 3/4 time signature have a GCF of 3, suggesting a connection between these rhythms.
Beyond the Basics: Exploring Further
The GCF concept extends beyond simple calculations. It connects to various mathematical fields, including:
1. Modular Arithmetic
In modular arithmetic, which deals with remainders after division, the GCF helps define the concept of congruence. Two numbers are congruent modulo a number if they leave the same remainder when divided by that number. The GCF plays a role in determining these congruences.
2. Number Theory
Number theory explores the properties of integers, including divisibility, prime numbers, and the GCF. It’s an area rich in theorems and unsolved problems, and the GCF is a fundamental building block for many investigations in this field.
3. Cryptography
Cryptography relies on mathematical concepts like GCF for secure communication. Algorithms such as the RSA algorithm, which uses prime factorization and the GCF, are used to encrypt and decrypt messages, ensuring their confidentiality.
Gcf 24 And 40
Conclusion
Our journey to discover the GCF of 24 and 40 has taken us through various computational methods, real-world applications, and its connections to other mathematical branches. The GCF is more than just a number; it’s a key concept that unlocks insights into numbers’ relationships, facilitates problem-solving, and underpins essential technologies. Whether you’re a student exploring the basics or a seasoned mathematician delving into advanced applications, the GCF remains a valuable tool that enhances your understanding of the world of numbers. Explore further, experiment with different numbers, and continue to unravel the fascinating world of mathematics where the seemingly simple can lead to profound discoveries.





