Remember that awkward moment in math class when you were asked to convert fractions to decimals? For me, it was always a struggle, especially when it came to fractions with larger denominators like 9/20. The process seemed daunting, but I soon discovered that it wasn’t as complicated as I thought. The key was to understand the fundamental relationship between fractions and decimals, and apply a simple method. This article will walk you through a step-by-step process to convert 9/20 into a decimal, along with helpful tips and insights to make the process easier for you.

Image: www.pinterest.com.au
Whether you’re a student tackling homework assignments, a professional needing to perform calculations, or simply curious about the world of numbers, understanding how to convert fractions to decimals can come in handy. This seemingly simple knowledge unlocks the door to a deeper understanding of mathematical operations and opens up possibilities in various fields.
Understanding the Basics of Fractions and Decimals
Before we dive into the conversion process, let’s revisit the fundamental definitions of fractions and decimals. A fraction represents a part of a whole, comprising a numerator (the number of parts you have) and a denominator (the total number of parts). Decimal numbers are a way of representing fractions using the base-ten system, where each digit’s position indicates its place value.
The core concept behind converting fractions to decimals is the idea of division. Dividing the numerator by the denominator transforms the fraction into a decimal representing the same value. For example, the fraction 1/2 is equivalent to 0.5. To understand this, think about half of a whole pie. Half a pie is the same as 0.5, or 50%, of the entire pie.
Step-by-Step Process: Converting 9/20 into a Decimal
Now, let’s apply this knowledge to convert 9/20 into a decimal. Here’s the step-by-step process:
- Divide the numerator by the denominator: In this case, divide 9 by 20.
- Perform the division: 9 ÷ 20 = 0.45.
- Result: 9/20 is equivalent to 0.45 in decimal form.
Additional Insights and Tips
While the conversion process itself is fairly straightforward, there are a few helpful tips to keep in mind:
- Simplifying fractions: If the numerator and denominator share a common factor, simplify the fraction before dividing. This can make the division process easier.
- Using a calculator: For larger fractions or more complex calculations, don’t shy away from using a calculator. It can streamline the process and ensure accuracy.
- Understanding place value: Remember that the decimal point separates the whole number part from the fractional part of a number. Each digit after the decimal point represents a decreasing power of 10.
For example, in the decimal 0.45, the ‘4’ represents 4 tenths (0.4), and the ‘5’ represents 5 hundredths (0.05). Understanding this place value concept enhances your comprehension of the decimal system and helps you interpret the results of your conversions.
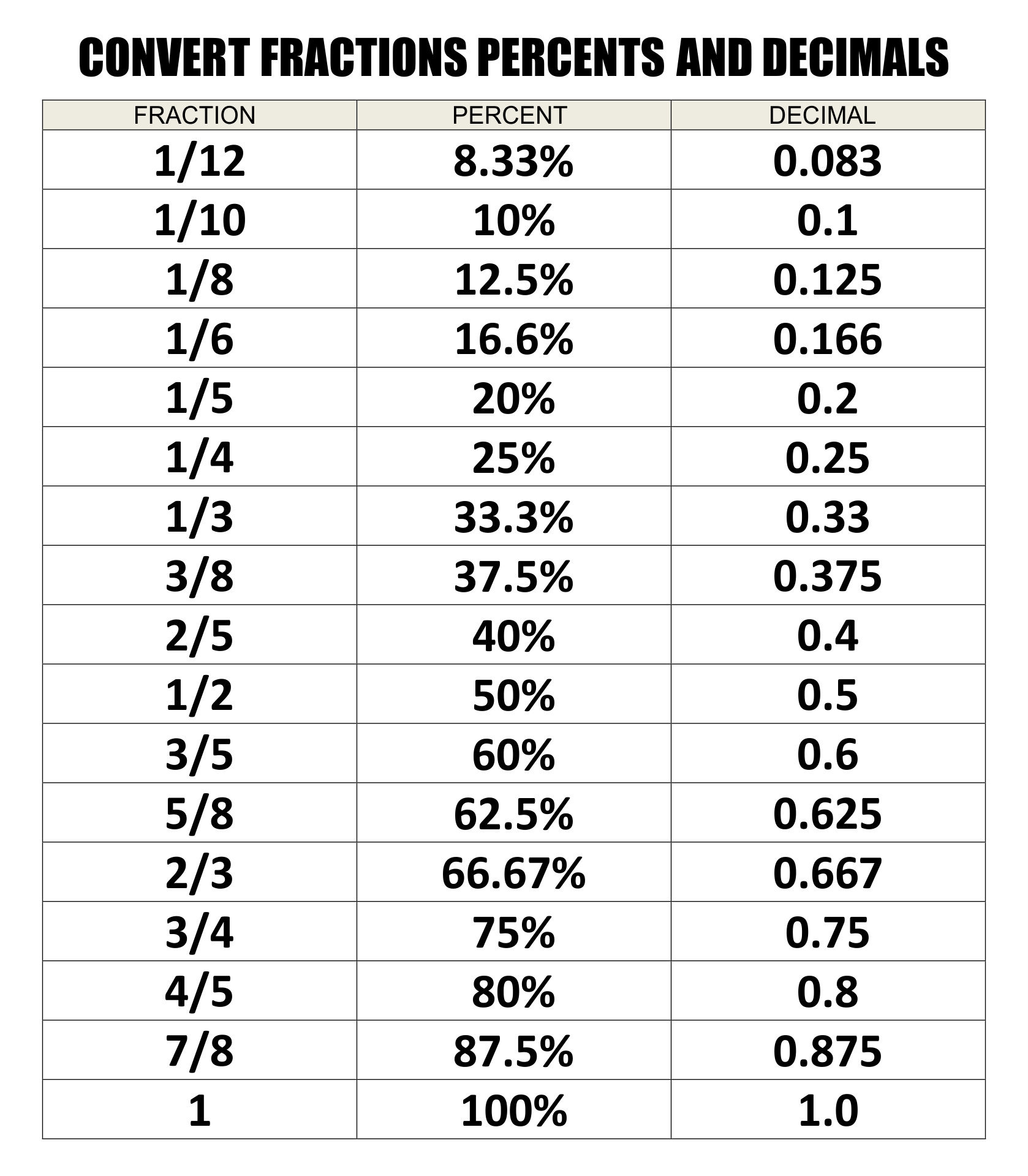
Image: www.vrogue.co
Real-World Applications
Converting fractions to decimals has various practical applications in different areas, including:
- Finance: Calculating interest rates, discounts, and other financial transactions often involve working with fractions and decimals.
- Measurement: Many measurement systems use both fractions and decimals, such as inches and centimeters.
- Science and Engineering: Data analysis, scientific experiments, and engineering calculations frequently involve converting fractions to decimals.
- Everyday life: Estimating quantities, sharing food, and calculating recipes often involve fractions and their decimal equivalents.
Examples
Let’s consider a few real-world examples:
- Finance: Calculate the amount of interest earned on a savings account with a 5% interest rate. 5% can be expressed as the fraction 5/100, which is equivalent to 0.05 in decimal form.
- Measurement: A carpenter needs to cut a piece of wood 1 1/2 inches long. This is equivalent to 1.5 inches in decimal form.
- Science: A chemist is working with a solution that is 9/20 of water. This means 45% or 0.45 of the solution is water.
FAQs
Here are some frequently asked questions about converting fractions to decimals:
Q1: What is the difference between fractions and decimals?
Fractions represent part of a whole, while decimals are a way to represent these fractions using the base-ten system. Fractions use a numerator and denominator, while decimals use a decimal point to separate whole numbers from the fractional part.
Q2: How do I convert a mixed number to a decimal?
To convert a mixed number like 1 1/2 to a decimal, you can first convert the fractional part (1/2) to a decimal (0.5) and then add it to the whole number part (1). So, 1 1/2 is equivalent to 1.5 in decimal form.
Q3: Can all fractions be converted to decimals?
Yes, every fraction can be converted to a decimal. However, sometimes the decimal representation may be infinite and repeating (like 1/3, which is 0.3333…).
9/20 Into A Decimal
Conclusion: Mastering Fractions and Decimals
Understanding how to convert fractions to decimals is a valuable skill that can benefit you in many aspects of life. Remember the basic concepts, follow the step-by-step process, and keep the helpful tips in mind. With a little practice, you’ll become comfortable working with both fractions and decimals and confidently navigate various mathematical calculations.
Are you interested in learning more about converting fractions to decimals? Do you have any particular challenges or questions related to this topic? Let me know in the comments section below!





