Have you ever stared at a complex three-dimensional shape, its volume a tantalizing riddle? Perhaps you’re a student grappling with calculus, or maybe you’re a curious mind seeking to understand the world around you. No matter your reason, the disc and washer methods are powerful tools that can unlock the secrets of volumes, and they are, at their core, a testament to the boundless creativity of mathematics. Today, we’re going to embark on a journey into the heart of these methods, exploring their nuances, their applications, and the magic they hold for understanding the world.
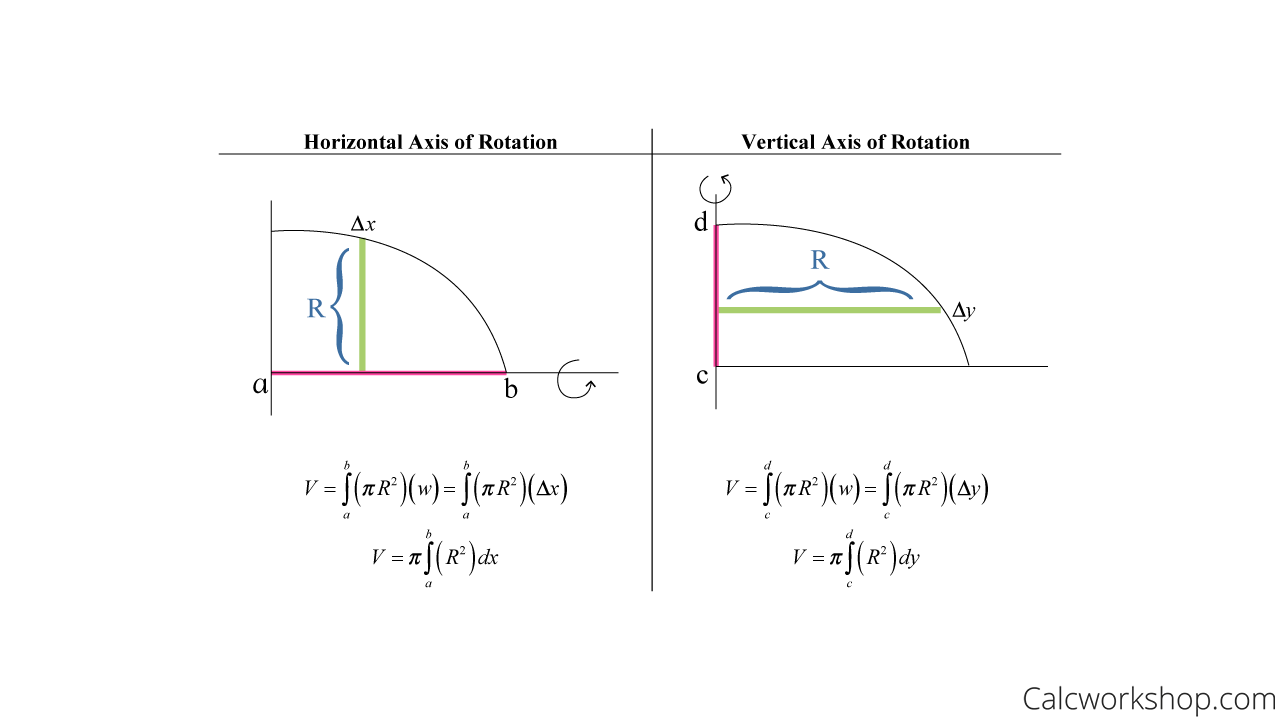
Image: officialbruinsshop.com
Imagine slicing through a solid object, perhaps a cone or a sphere, with a knife. Each slice, perfectly thin, reveals a cross-section, a glimpse into the inner workings of the shape. But what if we could use these slices to build the object back up again, to quantify its volume, to bring it to life through the power of math? That’s the essence of the disc and washer methods, both elegant solutions for calculating the volume of various three-dimensional shapes.
The Birth of a Concept: Understanding the Disc Method
Let’s begin with the disc method, a technique that revolves around the idea of spinning a two-dimensional shape around an axis to generate a solid. Imagine you have a function, a curve traced on the Cartesian plane, and you want to find the volume of the solid formed when this curve is spun around the x-axis.
The disc method works by dividing the solid into infinitesimally thin discs, each a perfect circle with a tiny thickness, Δ𝑥. The radius of each disc is simply the value of the function, f(𝑥), at the corresponding point on the curve. To discover the volume of each disc, we use the familiar formula for the volume of a cylinder: πr²h. In our case, the radius, r, is f(𝑥) and the height, h, is Δ𝑥. So the volume of a single disc is π[f(𝑥)]² Δ𝑥.
To find the total volume, we sum the volumes of all these infinitesimally thin discs. This summation translates into a definite integral, the fundamental tool of calculus. The integral of π[f(𝑥)]² with respect to 𝑥, from the starting point, a, to the ending point, b, along the x-axis, gives us the total volume.
Beyond the Basics: When Washers Come into Play
The washer method enters the scene when we encounter solids with holes, those that have a gap or hollow space within them. To visualize this, imagine spinning a region between two curves around an axis. This region is not a continuous solid but rather has a central void. This is where the washer method steps in, its ingenious design tailor-made for such intricate situations.
The washer method builds upon the concept of the disc, but instead of a single disc, it envisions a disc with a smaller disc “punched out” from its center. This hollowed-out disc, known as a washer, is what we use to calculate the volume of the region with the hole.
Consider two functions, f(𝑥) and g(𝑥), where f(𝑥) is always greater than g(𝑥) within the region of interest. When spinning this region around the x-axis, the outer radius of the washer corresponds to f(𝑥), while the inner radius is g(𝑥).
The volume of each washer is the difference between the volumes of two discs: one with radius f(𝑥) and another with radius g(𝑥). So, the volume of a single washer becomes π[f(𝑥)]² Δ𝑥 – π[g(𝑥)]² Δ𝑥. To find the total volume, we integrate this expression, π[f(𝑥)]² – π[g(𝑥)]² with respect to 𝑥, from the starting point, a, to the ending point, b.
Unlocking the Power of Visualization
Visualizing these methods is key to understanding their core mechanisms. A good first step is to plot the functions involved and carefully consider the axis of rotation. Imagine a pencil tracing the curve, and as the paper rotates around the axis, the pencil’s path creates the solid. Focus on the cross-sections, the “slices” of the solid, and you’ll see exactly how the disc or washer represents a single “slice.”
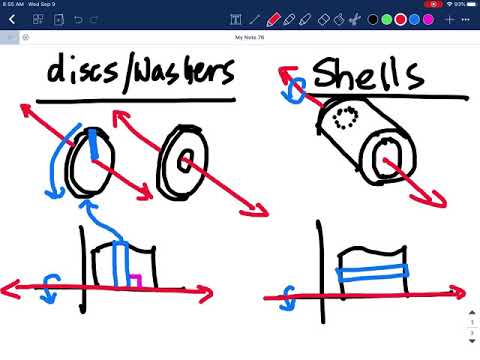
Image: www.youtube.com
Real-World Applications: From Engineering to Medicine
The disc and washer methods are not just theoretical exercises in calculus. They have real-world applications in diverse fields, impacting our lives every day.
- Engineering: Engineers use these methods to calculate the volume of complex structures, such as airplane wings or car parts. The accurate determination of volumes is crucial for designing efficient and safe structures.
- Medicine: Doctors and researchers employ these methods in medical imaging techniques, like Magnetic Resonance Imaging (MRI), to analyze the volume of organs and detect any abnormalities. These methods are invaluable in diagnosing and treating diseases.
- Architecture: Architects rely on these techniques to calculate the volume of buildings, ensuring efficient use of space, optimizing structural integrity, and facilitating the flow of people and resources.
Embracing the Power of Calculus
Mastering the disc and washer methods is not just about solving problems on a page. It’s about unlocking a new way of thinking, a way of understanding the world around us. By visualizing shapes, applying the principles of integration, and drawing connections to real-world scenarios, we can transcend the limitations of simple textbook problems and delve into the exciting world of practical applications.
Expert Insights and Actionable Tips
Dr. Emily Carter, a renowned mathematician, emphasizes the importance of visualization. “When you’re working with the disc and washer methods, don’t just rely on formulas. Draw the shapes, imagine them rotating, and try to see how the discs and washers fit together. This mental exercise will make the concepts much clearer,” she advises.
If you’re tackling these methods for the first time, don’t be discouraged by initial challenges. Practice is key! Start with simple examples, gradually increasing complexity as you gain confidence. There are many resources available online, such as interactive tutorials and practice problems, that can help you master the methods.
Disc Vs Washer Method
A Final Thought
The disc and washer methods are powerful tools, enabling us to calculate volumes, understand complex shapes, and solve real-world problems. They stand as a testament to the beauty and power of mathematics, a language that unveils the hidden secrets of our universe. So, embrace these methods, delve deeper into their mysteries, and discover the remarkable world that calculus can unveil.





