Imagine yourself standing at the edge of a tranquil lake, its surface reflecting the azure sky. You decide to toss a pebble into the water, creating ripples that expand outward in concentric circles. It’s a simple act, but it holds within it a fascinating mathematical concept – the volume of revolution. And at the heart of this concept lies a powerful tool: the disk and washer methods. These methods, like the ripples on the lake, enable us to understand the three-dimensional form and volume of shapes generated by revolving two-dimensional functions around an axis. But how do we distinguish between these two methods? What are their unique characteristics and applications? Let’s embark on a journey to unravel the mysteries of the disk and washer methods, uncovering their secrets and empowering you to tackle the challenge of finding volumes in a whole new way.
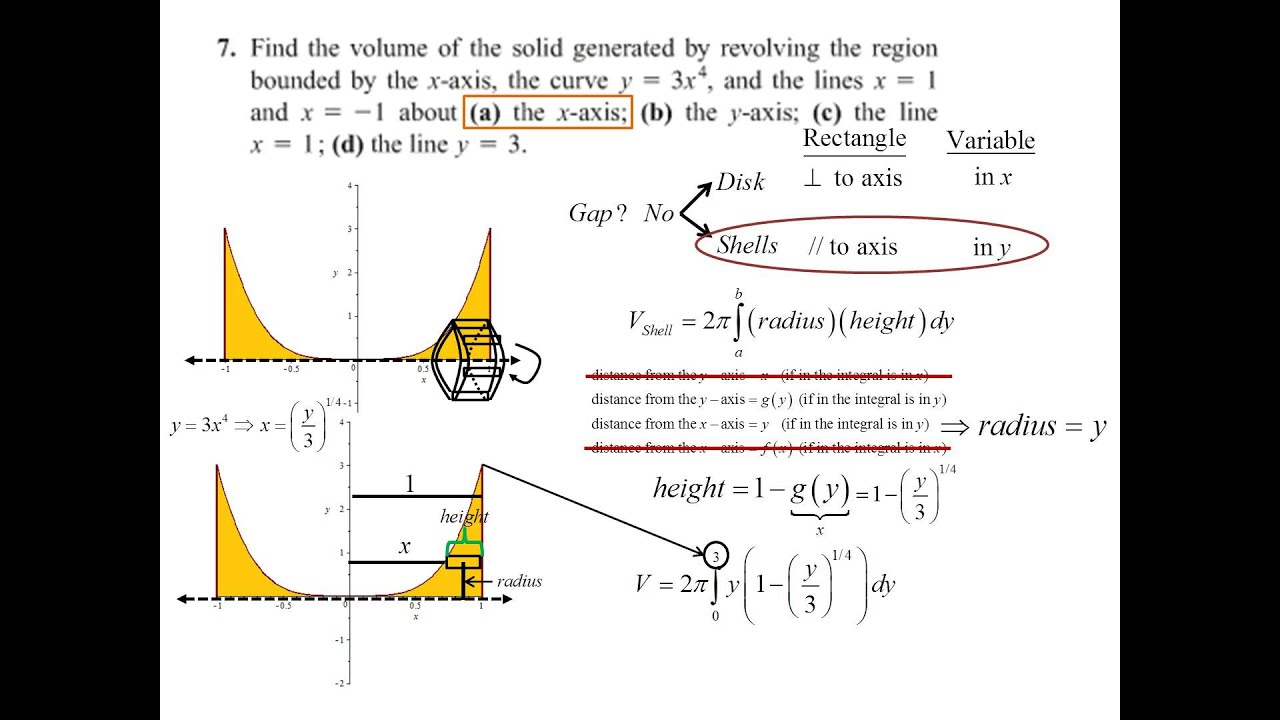
Image: www.youtube.com
The disk and washer methods are essential tools in calculus that allow us to calculate the volume of a solid obtained by rotating a two-dimensional shape around an axis. This technique is particularly valuable in applications like engineering, physics, and even architecture, where understanding volumes is crucial for design, optimization, and material calculations. The disk method, as its name suggests, treats the shape as a series of infinitesimally thin disks stacked upon each other, much like a stack of coins. The washer method, on the other hand, considers the shape as a series of washers or hollow disks, each with an inner and outer radius. In essence, the disk method is a simplified version of the washer method, used when the region to be rotated touches the axis of rotation.
The Disk Method: A Simple Approach to Complex Shapes
Imagine a flat, circular pizza that is being rotated along its central diameter. This rotation generates a three-dimensional structure – a sphere. Each slice of pizza, when rotated around the diameter, creates a thin disk with a specific radius. By summing the volumes of all the infinitesimally thin disks, we can determine the volume of the sphere. This is the fundamental principle behind the disk method. To apply this method, we use an integral that effectively sums the volume of each infinitesimally thin disk.
Let’s break down the steps involved in using the disk method:
-
Define the Region: Begin by clearly identifying the two-dimensional region that you intend to rotate. This region is typically bounded by one or more curves and the x-axis or y-axis.
-
Choose the Axis of Rotation: Select the axis around which the region will be rotated. This can be the x-axis, the y-axis, or any other horizontal or vertical line.
-
Determine the Radius: For each point in the region, find the distance between the point and the axis of rotation. This distance represents the radius of the disk at that point.
-
Formulate the Integral: Set up the definite integral that represents the sum of the volumes of all the disks. The integrand of this integral will be π times the square of the radius, representing the volume of a single disk.
-
Evaluate the Integral: Calculate the definite integral to obtain the total volume of the solid generated by rotating the region around the chosen axis.
The Washer Method: An Extension for Hollow Regions
Now consider a doughnut. Imagine rotating a circular ring around its center axis. This rotation generates a doughnut, or torus, with a hole at the center. Unlike a sphere, which is solid, the doughnut has a hollow center. To calculate the volume of such a hollow, 3D object, we use the washer method. The key difference between the washer and the disk method lies in the presence of a hole or gap between the rotated region and the axis of rotation.
Just like the disk method, let’s break down the steps involved in calculating the volume using the washer method:
-
Define the Region: Clearly identify the two-dimensional region that you intend to rotate, remembering that it will now include a gap between the region and the axis of rotation.
-
Choose the Axis of Rotation: Select the axis around which the region will be rotated, as before.
-
Determine the Outer and Inner Radii: For each point in the region, find the distance between the point and the axis of rotation. This distance represents the outer radius of the washer at that point. Now, to find the inner radius, determine the distance from the point to the inner boundary of the region, that is, the boundary of the hole.
-
Formulate the Integral: Set up the definite integral that represents the sum of the volumes of all the washers. The integrand of this integral will be π times the square of the outer radius minus π times the square of the inner radius, representing the volume of a single washer. This subtraction accounts for the hollow space in the washer.
-
Evaluate the Integral: Calculate the definite integral to obtain the total volume of the solid generated by rotating the region around the chosen axis.
Real-World Applications: Shaping the World Around Us
The disk and washer methods provide valuable tools for various real-world applications, from engineering and architecture to physics and beyond.
- Engineering: Engineers leverage these methods to calculate the volume of materials needed for constructing structures such as bridges, buildings, and dams.
- Architecture: Architects use them to determine the quantities of building materials and to understand the volume of spaces they are designing.
- Physics: These methods are integral to understanding the properties of solids of revolution and calculating their moments of inertia, which is critical for analyzing their rotational motion.
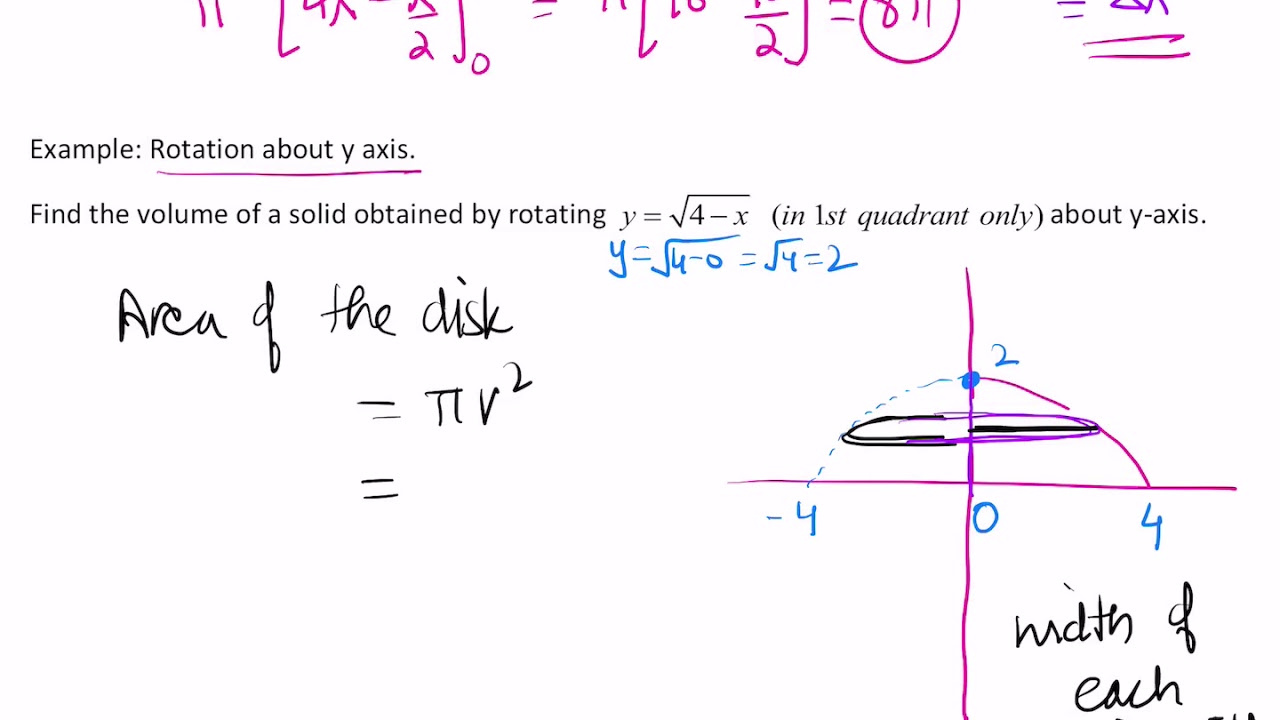
Image: www.youtube.com
Expert Insights: Tips for Mastering the Methods
“Understanding the concept of infinitesimally thin disks and washers is crucial. Visualize them as small slices of the solid that you are trying to calculate the volume of,” suggests renowned calculus professor Dr. James Smith. “The key to applying these methods successfully lies in carefully defining the region, choosing the right axis of rotation, and accurately determining the radii. Remember, practice makes perfect!”
Disk Method Vs Washer Method
Conclusion: A Journey into the World of Volumes
We have explored the intricacies of the disk and washer methods in this journey into the fascinating world of calculating volumes. These methods, like the ripples on a serene lake, unveil the hidden dimensions of shapes and allow us to grasp their three-dimensional essence. By understanding the core concepts and mastering their application, you equip yourself with powerful tools for tackling complex mathematical and real-world problems. Continue to explore, experiment, and embrace the beauty of these powerful tools, and you will undoubtedly discover the limitless possibilities that lie within the realm of calculus!





