Have you ever wondered what makes a swing swing or a pendulum sway? The answer lies in a fascinating realm of physics called oscillations, where the world around us dances to a rhythmic beat. But there’s a subtle yet crucial distinction in how we describe this rhythm – a difference between the familiar concept of frequency and the often-overlooked angular frequency.
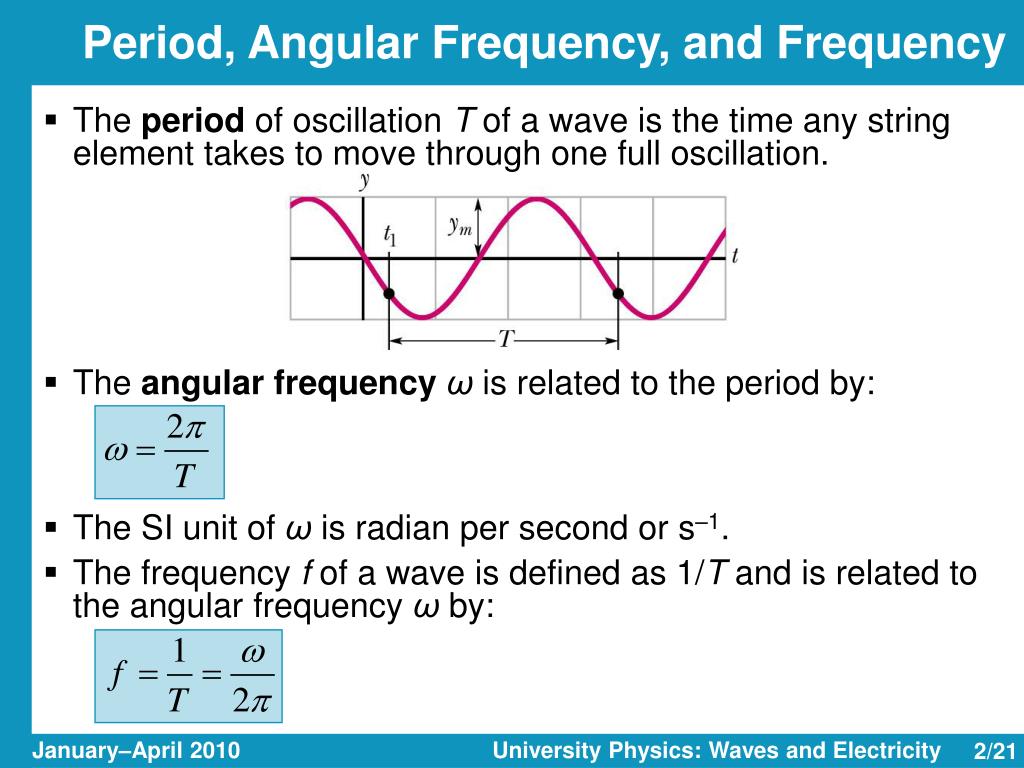
Image: haipernews.com
Whether it’s the gentle swaying of a chandelier or the pulsating light of a laser, oscillations are ubiquitous in our lives. Understanding the difference between frequency and angular frequency allows us to delve deeper into the complexities of these rhythmic movements, unlocking the secrets of their behavior and the forces that govern them.
Unveiling the Rhythm: Frequency and Its Role in Oscillations
Imagine a bouncing ball. It goes up and down, repeating its motion at a certain pace. This pace, the number of times the ball bounces up and down in a given timeframe, is what we call frequency. It’s measured in Hertz (Hz), representing the number of cycles per second.
So, if our bouncy ball completes one full bounce every second, its frequency is 1 Hz. If it bounces twice a second, its frequency is 2 Hz, and so on. Frequency is a way of characterizing the tempo of oscillations, telling us how fast they repeat themselves.
A Deeper Look: Angular Frequency and its Connection to Circular Motion
Now, let’s consider a slightly different scenario. Instead of a bouncing ball, imagine a point moving in a circle. This point, as it traces its path, also exhibits a rhythmic pattern, completing a full circle at a specific pace. This pace, however, is measured not in the number of cycles per second but in the number of radians per second. It’s called ‘angular frequency’ and is denoted by the Greek letter ω (omega).
But why radians? Radians are a unit of angular displacement, representing the ratio of a circle’s arc length to its radius. This is where the connection to circular motion comes in. Angular frequency describes how fast a point rotates in a circle, measured in radians per second.
Bridging the Gap: Connecting Frequency and Angular Frequency
Though they seem distinct, frequency and angular frequency are intimately related. They both describe the rhythm of oscillations, but they focus on different aspects of this rhythm. Think of it this way:
- Frequency (f) tells you how many complete cycles occur in a second. It’s like the tempo of a song, measured in beats per minute.
- Angular frequency (ω) tells you how quickly the angle of the oscillating object changes in a second. It’s like the speed of a spinning record, measured in revolutions per minute.
The key connection lies in the fact that for a single cycle, an object covers 2π radians (a full circle). Therefore, we can relate frequency and angular frequency using the following simple equation:
ω = 2πf
This equation tells us that angular frequency is essentially 2π times the regular frequency. This relationship is fundamental in understanding the relationship between oscillations and circular motion, playing a crucial role in many areas of physics.
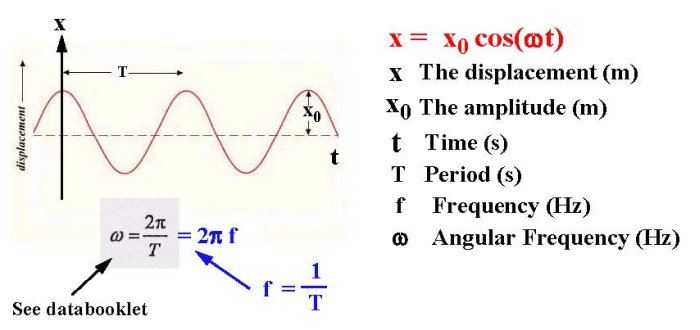
Image: evelineessay.web.fc2.com
Beyond the Basics: Angular Frequency in Real-World Applications
Angular frequency isn’t just a theoretical concept; it finds numerous applications in real life. Here are a few examples:
- Simple Harmonic Motion: A mass attached to a spring and oscillating back and forth exhibits simple harmonic motion. The period of this oscillation depends on the angular frequency, which is determined by the mass and the spring constant.
- Radio Waves: Radio waves are electromagnetic waves that oscillate at specific frequencies. Understanding their angular frequency is essential in designing radio transmitters and receivers.
- Electrical Circuits: In alternating current (AC) circuits, the angular frequency of the voltage and current determines the electrical behavior of the circuit.
- Vibrating Strings: The fundamental frequency of a vibrating string, like those in musical instruments, is directly related to the angular frequency of the wave traveling along the string.
Expert Insights: Understanding Angular Frequency is Key
As renowned physicist Richard Feynman once said, “If you want to understand a thing, you must study it in motion.” Angular frequency is the key to understanding motion in many areas of physics, from the intricate world of atoms to the vast expanse of the cosmos. It allows us to analyze the inherent rhythm of a wide range of phenomena, from the simple sway of a pendulum to the complex oscillations of light waves.
Actionable Tips: Harnessing the Power of Angular Frequency
- Visualize the Motion: When dealing with oscillations, try to imagine the object’s movement in a circular path. This can help to grasp the concept of angular frequency and its connection to circular motion.
- Focus on the Relationship: Remember the equation ω = 2πf and use it to convert between frequency and angular frequency. This will help you in understanding the interconnectedness of these concepts.
- Explore the Applications: Delve deeper into the various applications of angular frequency in different fields. This will help you appreciate its significance in real-world scenarios.
Angular Frequency Vs Frequency
Conclusion: The Rhythm of Life, Explained
From the rhythmic sway of a simple pendulum to the complex oscillations of light waves, angular frequency plays a vital role in shaping our understanding of the physical world. By understanding the difference between frequency and angular frequency, we can peek behind the curtain of oscillations and gain a deeper appreciation for the fundamental rhythms that govern our universe. So, the next time you witness a rhythmically oscillating phenomenon, remember the subtle but powerful forces at play, and the fascinating world of angular frequency.





