Growing up, I always loved geometry. The way shapes could be manipulated and transformed fascinated me. I remember spending hours drawing quadrilaterals, specifically trapezoids and rhombuses. As I delved deeper, a question lingered in my mind: “Is a rhombus a trapezoid?” The answer, as I later discovered, isn’t as straightforward as it might seem.
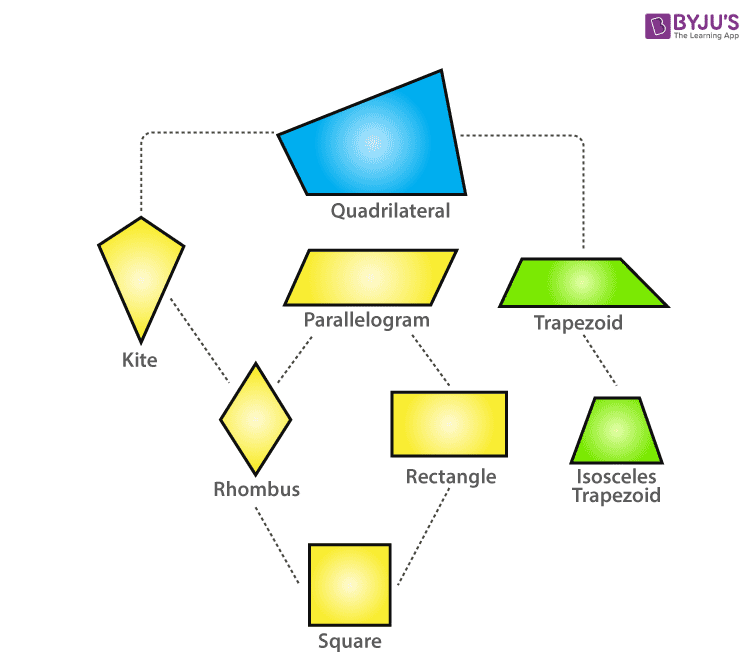
Image: byjus.com
To understand the relationship between these shapes, we need to explore the world of quadrilaterals. Quadrilaterals, simply put, are four-sided polygons. With their diverse properties, quadrilaterals come in various flavors – squares, rectangles, parallelograms, trapezoids, and more. Today, we’ll focus our attention on the relationship between rhombuses and trapezoids.
Unveiling the Properties: Rhombuses and Trapezoids
A rhombus is a quadrilateral with all four sides equal in length. It’s a special type of parallelogram, meaning its opposite sides are parallel, and its opposite angles are equal. A trapezoid, on the other hand, is a quadrilateral with at least one pair of parallel sides. Unlike a rhombus, a trapezoid doesn’t have the same requirement for all sides being equal.
The key to understanding the relationship lies in these definitions. Here’s the crucial point: since a rhombus has two sets of parallel sides, it automatically fulfills the condition for a trapezoid. Therefore, every rhombus can be classified as a trapezoid. However, the reverse is not always true.
Understanding the Relationship: Every Rhombus is a Trapezoid, but Not Every Trapezoid is a Rhombus
Think of it like this: All squares are rectangles, but not all rectangles are squares. Similarly, all rhombuses are trapezoids, but not all trapezoids are rhombuses. The reason lies in the additional properties a rhombus possesses that a trapezoid may or may not have.
A rhombus has several properties that set it apart from a general trapezoid. These include:
- All sides equal: While a trapezoid requires only one pair of parallel sides, a rhombus must have all four sides equal.
- Diagonals bisect each other at right angles: The diagonals of a rhombus intersect at a 90-degree angle, a property not necessarily true for all trapezoids.
- Opposite angles are equal: This is a property common to both parallelograms and rhombuses but not to all trapezoids.
Key Takeaways and Insights: A More In-Depth Look
The relationship between rhombuses and trapezoids might seem complex, but it’s actually quite straightforward. The key is understanding the defining properties of each shape. A rhombus is a special type of trapezoid because it fulfills the minimum requirement of having at least one pair of parallel sides. While all rhombuses are trapezoids, the same cannot be said in reverse.
This understanding is crucial in various fields, including:
- Geometry: Studying the relationship between different shapes helps develop a deeper understanding of geometric principles.
- Architecture: Architects often use trapezoids and rhombuses in their designs, understanding their properties is vital for structural integrity.
- Engineering: Engineers rely on geometric principles to create efficient and safe structures. Understanding the differences and similarities between shapes allows for more informed design decisions.

Image: bartowtrc.org
Expert Tips: Recognizing and Differentiating
Here are some tips to help distinguish between a rhombus and a trapezoid:
- Check for parallel sides: Both shapes have at least one pair of parallel sides.
- Measure side lengths: If all four sides are equal, it’s a rhombus.
- Look for right angles: The diagonals of a rhombus intersect at right angles.
- Consider the angles: The opposite angles of a rhombus are equal.
Remember, a rhombus is also a parallelogram, so it shares the characteristics of a parallelogram. If you can identify the properties of a parallelogram, you’re well on your way to understanding why every rhombus is a trapezoid.
Frequently Asked Questions
Q1: What is the difference between a rhombus and a trapezoid?
The key difference lies in the number of equal sides. A rhombus has all four sides equal, while a trapezoid only requires one pair of parallel sides. All rhombuses are trapezoids, but not all trapezoids are rhombuses.
Q2: Are all parallelograms trapezoids?
Yes, all parallelograms are trapezoids. Parallelograms have two pairs of parallel sides, fulfilling the requirement of a trapezoid. However, not all trapezoids are parallelograms.
Q3: Can a trapezoid be a rhombus?
No, a trapezoid cannot be a rhombus unless it has all four sides equal. While a rhombus is always a trapezoid, the reverse is not always true.
Q4: What are some real-world examples of rhombuses and trapezoids?
Rhombuses are found in the shape of diamonds, some road signs, and some kites. Trapezoids are often used in symmetrical structures like bridges and buildings. Look closely at your surroundings, and you’ll find that these shapes are all around us.
A Rhombus Is A Trapezoid
Conclusion: Embracing the Diversity of Shapes
Understanding the relationship between rhombuses and trapezoids is essential for navigating the world of geometry. Recognizing that every rhombus is a trapezoid but not vice versa requires understanding the defining properties of each shape. As you explore the fascinating world of geometry, remember that shapes are more than just lines and angles; they hold a wealth of knowledge and real-world applications. Exploring these relationships can deepen our understanding of the world around us.
Are you interested in learning more about rhombuses, trapezoids, and other quadrilaterals? Share your thoughts and questions in the comments below. Let’s continue this fascinating journey of discovery together!





